Teori Bahasa & Automata
1. Finite State Automata
Finite State Automata adalah mesin abstrak berupa sistem model matematika yang dapat menerima input dan mengeluarkan output yang memiliki state berhingga banyaknya, dan dapat berpindah dari satu state ke state lainnya berdasarkan input dan fungsi transisi.
Finite State Automata memiliki bentuk formal dengan 5 buah tupel, yaitu :
M = (Q, Σ, 𝛅, A, F)
Ket :
1. Q = Himpunan State
2. Σ = Himpunan Simbol Input
3. 𝛅 = Fungsi Transisi
4. A = State Awal
5. F = Final State
M = (Q, Σ, 𝛅, A, F)
Ket :
1. Q = Himpunan State
2. Σ = Himpunan Simbol Input
3. 𝛅 = Fungsi Transisi
4. A = State Awal
5. F = Final State
M = (Q, Σ, 𝛅, A, F)
------------------------
Diketahui :
Diketahui :
M ={ q0, q1 , q2, q3, q4 , q5 }
Σ = { 1,2,3 }
𝛅 =
A = {q0}
F = {q5}
Uji Input String dari mesin FSA diatas :
M = (Q, Σ, δ, S, ∆, λ)
Ket :
1. Q = Himpunan State
2. Σ = Himpunan Simbol Input
3. 𝛅 = Fungsi Transisi
4. S = State Awal
5. ∆ = Himpunan Output
6. λ = Fungsi Output untuk setiap State
Berikut adalah gambar dari Mesin Moore :
M = (Q, Σ, δ, S, ∆, λ)
----------------------------
Diketahui :
M ={ q0, q1 , q2, q3, q4 }
Σ = { 0,1}
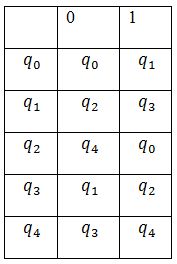
𝛅 =
S = {q0}
∆ = {0, 1, 2, 3, 4}
λ = λ(q0) = 0; λ(q1) = 1; λ(q2) = 2; λ(q3) = 3; λ(q4) = 4;
Uji input biner :
b. 9 mod 5 = 4 (biner 9 = 1001)
Σ = { 1,2,3 }
𝛅 =
A = {q0}
F = {q5}
Uji Input String dari mesin FSA diatas :
- Uji menggunakan 'Multiple Run'
- Uji menggunakan 'Fast Run'
2. Mesin Moore
Mesin moore adalah mesin yang menghubungkan nilai output dengan masing-masing state. Mesin moore didefinisikan dalam 6 buah tupel, yaitu :M = (Q, Σ, δ, S, ∆, λ)
Ket :
1. Q = Himpunan State
2. Σ = Himpunan Simbol Input
3. 𝛅 = Fungsi Transisi
4. S = State Awal
5. ∆ = Himpunan Output
6. λ = Fungsi Output untuk setiap State
Berikut adalah gambar dari Mesin Moore :
M = (Q, Σ, δ, S, ∆, λ)
----------------------------
Diketahui :
M ={ q0, q1 , q2, q3, q4 }
Σ = { 0,1}
𝛅 =
S = {q0}
∆ = {0, 1, 2, 3, 4}
λ = λ(q0) = 0; λ(q1) = 1; λ(q2) = 2; λ(q3) = 3; λ(q4) = 4;
Uji input biner :
- Uji menggunakan 'Multiple Run' :
a. 10 mod 5 = 0 (biner 10 = 0101)
b. 6 mod 5 = 1 (biner 6 = 0110)
c. 17 mod 5 = 2 (biner 17 = 10001)
d. 9 mod 5 = 4 (biner 9 = 1001)
e. 33 mod 5 = 3 (biner 33 = 100000
- Uji menggunakan 'Fast Run' :
a. 10 mod 5 = 0 (biner 10 = 0101)
Lembar jawaban mata kuliah teoti bahasa & autonata :












Komentar
Posting Komentar