REGULAR GRAMMAR
Grammar adalah bentuk abstrak yang dapat diterima untuk membangkitkan suatu kalimat otomata berdasarkan suatu aturan tertentu. Grammar dapat didefiniskan dengan 4 Tupel, yaitu :
G = {V,T,P,S}
ket :
V = Himpunan Simbol Variabel
T = Himpunan Simbol Terminal
P = Kumpulan Aturan Produksi
S = Simbol Awal
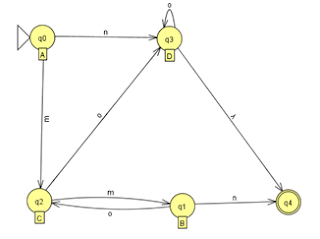
Berikut adalah mesin abstrak Grammar yang kami buat dengan produksi sebagai berikut :
Production
Convert to FA
Setelah membuat mesin abstrak Grammar diatas, sekarang akan kita tentukan bentuk formal dari 4 Tupel yang sudah dijelaskan diatas.
1. Bentuk Formal Regular Grammar
V = {A,B,C,D}
T = {M,N,O}
P = {A→mC, A→nD, B→oC, C→mB, C→oD, D→oD, B→n, D→𝞴}
S = q0
Dapat di simpulkan Bentuk Formal Regular Grammar dari mesin abstrak diatas adalah
G =({A,B,C,D},{M,N,O},P = {A→mC, A→nD, B→oC, C→mB, C→oD, D→oD, B→n, D→𝞴}, q0}
---------
Hasil mesin abstrak diatas yang sudah di convert ke FA dapat juga kita tulis dalam bentuk formal FSA, yang memiliki 5 Tupel antara lain :
M = (Q, Σ, 𝛅, A, F)
Ket :
Q = Himpunan State
Σ = Himpunan Simbol Input
𝛅 = Fungsi Transisi
A = State Awal
F = Final State
Σ = {M,N,0}
𝛅 = Fungsi Transisi
A= q0
F= q4
Dapat disimpulkan bentuk formal FSA dari mesin abstrak diatas adalah
M= ( {q0 , q1 , q2 , q3, q4}, {M,N,0}, 𝜹 , q0 , {q4})
---------------------------------------------------------------------------------------------------------------------------------------
Link bahan presentasi kelompok 2 : https://drive.google.com/open?id=1BQW7Hsy1c9_xhOven5z1r-9Ucj_vAHL6
Anggota Kelompok :
1. Dian Aprilia Utami
2. Kharisma Edo Winarno
3. Mohamad Nurul



Komentar
Posting Komentar